Поведение потребителя в условиях рисковой неопределенности
Под рисковой неопределенностью (риском) будет пониматься ситуация, когда лицу, принимающему решения, известны все будущие исходы развития ситуации и для каждого исхода известна его вероятность. Число исходов может быть как конечным, так и бесконечным. Более того, множество исходов может быть непрерывным интервалом; в последнем случае уместнее говорить о функции распределения вероятностей исходов, а не о вероятностях конкретных исходов.
В неоклассической экономической теории поведения потребителя, основанной на теории полезности, с одной стороны, само по себе наличие риска обладает полезностью (положительной или отрицательной), а с другой - ожидаемая полезность при реализации риска отличается от полезности ожидаемого исхода. Например, половина полезности двух одинаковых автомобилей почти для всех людей ниже полезности одного автомобиля, поэтому никто не играет на автомобиль в подбрасывание монетки.
Поясним. Подбросив монетку, Вы либо с вероятностью 0,5 теряете свою машину - и ваша полезность равна нулю; либо с той же вероятностью становитесь обладателем двух авто. Следовательно, ожидаемая полезность равна половине полезности двух автомобилей; но при этом ожидаемый исход игры - один автомобиль и, следовательно, полезность ожидаемого исхода - полезность одного автомобиля.
Поскольку деньги имеют собственную полезность, хотя для каждого человека она своя, то можно измерять полезность риска в денежных единицах и говорить о плате (которую человек согласен внести) за отказ от риска либо, наоборот, о плате за приобретение риска. Соответственно людей, готовых платить за то, чтобы избежать риска, называют "избегающими риска" (risk averse), а готовых платить за риск - "любителями риска" (risk lovers).
Обычно считается, что с ростом величины риска (мы пока не уточняем, что это такое) растет и плата за риск или отказ от него. (См. рис. 1). При этом обычно полагается, что скорость этого роста возрастает с ростом величины риска, но нельзя считать невозможными и другие варианты: скорость роста может быть постоянной или убывать.
Точно также нельзя считать невозможным и то, что человек, который любит небольшой риск, например из-за того, что сам факт наличия риска имеет для него ценность, предпочтет отказаться от большого риска. (См. рисунок 2.) Например, человек играет в лотерею, но при этом страхует свое имущество - два риска, но противоположная реакция.
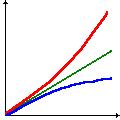
Рис. 1. Зависимость платы за отказ от риска от величины риска
По горизонтальной оси отложена величина риска, по вертикальной оси - плата за отказ от риска для "лица, избегающего риска" - слева и для "любителя риска" - справа. На обоих графиках показаны три варианта зависимости платы за отказ от риска от величины риска: красным цветом если скорость роста платы за отказ от риска растет; зеленым - остается постоянной; синим - убывает.
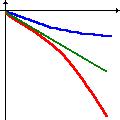
Рис. 2. Превращение "любителя риска" в "избегающего риска"
Здесь представлена зависимость платы за отказ от риска от величины риска. На рисунке показано, что у двух различных людей момент превращения из "любителя риска" в избегающего риска может происходить при разной величине риска - при меньшей (синий график) или при большей (красный). Отметим, что при нулевой величине риска плата за него - нулевая.
Итак, для прогноза поведения конкретного потребителя при наличии риска нужно уметь определять скорость роста платы за риск или отказ от него. Причем желательно знать, как эта скорость меняется при росте величины риска.
Теперь переходим к вопросу об измерении величины риска. Поскольку рисковая неопределенность задается функцией распределения исходов рисковой ситуации, то величина риска определяется функцией распределением риска. Другими словами, величина риска есть значение некоторого функционала, определенного на множестве функций распределения риска. И весь вопрос заключается в выборе функционала.
Наиболее часто в качестве меры риска используются стандартное отклонение и дисперсия исходов рисковой ситуации. Однако утверждать, что именно один из этих двух параметров является мерой риска в действительности, нельзя. Даже если мы основываемся только на анализе моментов распределения риска, то мы обязательно должны проверять, зависит ли определяемая человеком величина риска от старших моментов распределения и в первую очередь - от третьего момента (от асимметрии распределения риска).
Итак, для определения склонности человека к риску и платы, на которую он согласен, дабы избежать риска, нужно выяснить:
1.Ценен ли для человека риск сам по себе? То есть является ли человек любителем риска вообще или хотя бы при его малых величинах?
2.С какой скоростью растет плата за отказ от риска при росте его величины?
3.Как эта скорость изменяется?
4.Как влияет асимметрия распределения исходов рисковой ситуации на оценку человеком величины риска?
Это минимальный перечень вопросов. Сюда можно сверх этого добавить дополнительные вопросы об изменениях скорости роста платы за отказ от риска и вопросы о влиянии на оценку индивидуумом величины риска моментов распределения риска более высокого порядка.
Вопросы, задаваемые потребителю, и пояснения к ним
Здесь приводится перечень вопросов из нашего теста "Нужно ли Вам страхование?", направленных на определение склонности человека к риску. И даются пояснения относительно целей, с которыми задаются эти вопросы.
1)Вы играете в азартные игры или лотереи? Ответ "Да" позволяет сказать, что человек является любителем риска, по крайней мере при небольшой величине риска.
1А) Вы играете в азартные игры часто, делаете крупные ставки и не слишком обращаете внимание на проигрыш? Ответ "Да" означает, скорее всего, что опрашиваемый является любителем риска и ему можно советовать рассматривать любой риск в жизни как еще одну азартную игру. Ответ "Нет" говорит, что человек - любитель маленьких рисков, крупных рисков он избегает.
1Б) Какую максимальную ставку Вы могли бы сделать в азартной игре, например при подбрасывании монетки? Данный вопрос позволяет определить величину риска при которой "любитель маленького риска" превращается в "избегающего риск".
2) Предположим ситуация такая: Вы можете потерять или получить сумму с вероятностью 50%. Сколько Вы заплатите, чтобы избежать этого риска? Данный вопрос позволяет судить о скорости роста платы за отказ от риска и построить линейную зависимость платы за риск от величины риска. Сумма зависит от: а) дохода индивидуума, б) ответа на вопрос 1Б. Вероятность 50% определяется тем, что нам нужно распределение риска обладающее симметричностью.
3) Теперь Вы можете потерять или получить двойную сумму с вероятностью 50%. Сколько вы заплатите, чтобы избежать этого риска? Этот вопрос - вспомогательный - нужен для улучшения точности измерения влияния эксцесса на оценку опрашиваемым величины риска.
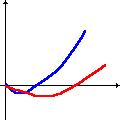
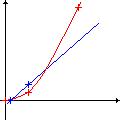
Рис. 3. Построение зависимости по двум и трем точкам
Синий цвет- зависимость для "любителя маленького риска", построенная по двум точкам. Видно, что плата за отказ от риска становится отрицательной при малом риске.
Красный цвет - зависимость платы за отказ от риска от величины риска для "лица, избегающего риска", построенная по трем точкам.
4) Теперь Вы можете потерять или получить десятиричную сумму с вероятностью 50%. Сколько Вы заплатите, чтобы избежать данного риска? Этот вопрос позволяет определить изменение скорости роста платы за риск и позволяет построить квадратичную модель зависимости платы за риск от величины риска. (См. рис. 3).
5) Теперь ситуация несколько иная. Вы можете получить половинную сумму с вероятностью 80% и потерять двойную сумму с вероятностью 20%. Сколько Вы заплатите, чтобы избежать этого риска? В данном вопросе распределение риска асимметрично. Поэтому мы можем определить зависимость оценки риска, даваемой индивидуумом, от асимметрии распределения. (Предполагается линейность зависимости. При построении зависимости платы за риск от асимметрии нужно не забывать о вкладе стандартного отклонения в плату за риск).
Как результат этого опроса может быть сделан вывод, что человек является "любителем риска" либо построена модель зависимости платы за отказ от риска, на которую он согласен, от величины риска вида:
P = A1 (s + Ba) + A2 (s + Ba)2 + P0
Здесь Р - плата за риск; Р0 - параметр, который можно назвать "плата за нулевой риск"; s - стандартное отклонение распределения риска; a - асимметрия распределения риска; A1 ; A2 ; B - параметры модели.
Меню

 Allinsurance.kz
Казахстанский портал о страховании
Allinsurance.kz
Казахстанский портал о страховании
29
Пт, авг