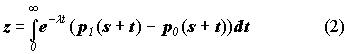Оптимальная страховая защита в случае страхования с BMS.

В этой статье будут получены несколько новых выводов для договоров страхования с BMS, которые будут сравнены с соответствующими результатами для стандартных договоров страхования. Теоретической основой для этой статьи служит модель ожидаемой полезности, для которой будут рассмотрены оптимальная страховая защита для фиксированной функции премии и оптимальная по Парето страховая защита. Данная работа является продолжением другой работы того же автора, где были разработана концепция поведения потребителя при наличии BMS в договоре страхования. 

Ключевые слова.

Договор страхования.
Система Бонусов и Штрафов (Бонус-Малус, BMS).
Оптимальная страховая защита.
Франшиза.
Теория Полезности.
Оптимальность по Парето.

1. Введение

Должен или не должен потребитель покупать страхование? Если должен, тогда какую страховую защиту он должен предпочесть? На практике эти фундаментальные вопросы являются основными в сфере купли-продажи страхования и подвергались всестороннему изучению в разных условиях во множестве работ по страховому экономиксу. Классическими здесь можно признать следующие работы: Mossin (1968), Arrow (1974) и Raviv (1979). Общим для этих работ было то, что в них все внимание было сосредоточено на договорах страхования без индивидуальных поправок к премиям, связанных с индивидуальной статистикой убытков. Однако, и с точки зрения страхователя, и с точки зрения экономической теории, договор страхования, в которых имеется BMS, являются гораздо более сложным случаем, если мы рассматриваем их с целью оптимизации страховой защиты. Увеличение сложности связано с действием механизма бонусного голода, т.е. стремлением страхователей оплачивать мелкие убытки самостоятельно, чтобы избежать повышения премий в дальнейшем. Предназначение этой статьи – включить механизм бонусного голода в модели оптимальной страховой защиты при наличии BMS в договорах страхования. Данная работа является продолжением другой работы, где были разработана концепция поведения потребителя в момент возникновения убытка при наличии BMS в договоре страхования.

Работа имеет следующую структуру: Секции 2 и 3 описывают стандартный договор страхования, а также подход к решению задача оптимизации страховой защиты, основанный на ожидаемой полезности. В Секциях 4 – 6 будут получены некоторые новые результаты в вопросе об оптимальной страховой защите при наличии BMS. Полученные результаты будут сравнены с результатами для стандартного договора страхования. В Секции 5 рассматривается оптимальная страховая защита при фиксированной функции премии, а в Секции 6 будет рассмотрена Парето оптимальная защита. В Секции 7 полученные результаты будут суммированы.

2. Обобщенный договор страхования.

Напомним вкратце основные свойства обобщенного договора имущественного страхования с BMS, как это было представлено в Holtan(2001). Рассмотрим страхователя, который передает в страхование риск Х, где Х – случайная величина, имеющая функцию плотности распределения f(x) при х³0. Со стороны ущерба данный договор характеризуется оговоренным в нем страховым возмещением с(х) и реальным возмещением с^*(х), выплачиваемыми при возникновении убытка Х=х:

c^*(x) = c(x) – z при c(x) > z ; иначе c^*(x) = 0         (1)

Функция реального страхового возмещения c^*(x) является функцией действительно выплачиваемого возмещения, поскольку учитывает компонент потери бонуса z. В то же время оговоренное договором возмещение c(x) есть просто величина убытка, минус оговоренная франшиза. Детерминированная, индивидуальная для каждого страхователя, величина z есть точка эксцедента, начиная с которой страхователь должен сообщать страховщику об убытке, если он выбрал оптимальную стратегию бонусного голода после возникновения убытка. Другими словами z есть настоящая стоимость потерянного бонуса, определяемая таким образом:

Где l – детерминистическая рыночная процентная ставка для самофинансирования убытка; p₁(s + t) – премия уплачиваемая в момент времени t после возникновения убытка в момент s; а p₀(s + t) – премия, соответственно, если убытков не было. Процессы премий p₁(s + t) и p₀(s + t) считаются непрерывными и детерминированными для любого t>0. Больше информации об эффектах BMS в договоре страхования можно найти в предыдущей статье.

Важным выводом, который частично вытекает из (1) и (2) является то, что независимо от функции договорного страхового возмещения функция реального страхового возмещения всегда имеет индивидуальную для каждого страхователя франшизу, см. Предложение 2 из Holtan (2001). Как мы увидим позднее, это свойство объясняет большинство характеристик оптимальной страховой защиты, которые выведены в этой статье.

3. Подход, основанный на ожидаемой полезности.

Существование функции реального страхового возмещения явным образом будет влиять на индивидуальный выбор страхового покрытия, представленного в виде договора с BMS. Возвратимся к нашему основному вопросу из Секции 1: Должен ли потребитель покупать страхование, и какую страховую защиту он при этом предпочтет. Или более точно: Какова оптимальная страховая защита для рассматриваемого потребителя. Как говорилось ранее, эти вопросы традиционно рассматриваются в рамках страхового экономикса, в общем этот вопрос можно найти в Borch (1990), главы 2.1, 2.9, 6.3 и 6.4 или в более новом и улучшенном издании Aase (1993), глава 8. Вкратце этот, ставший классическим, подход можно суммировать следующим образом:

Рассмотрим потребителя страховой услуги и договор страхования описанный в Секции 2. Положим, w – есть исходное богатство потребителя. Предположим также, что рисковые предпочтения потребителя описываются функцией ожидаемой полезности Eu(.), т.е. если потребитель делает выбор в условиях неопределенности он стремится максимизировать ожидаемую полезность своего богатства. Точнее, потребитель предпочтет неопределенное богатство W₁ другому неопределенному богатству W₂, если Eu(W₁) ³ Eu(W₂). Период на который ориентируется потребитель при принятии решений будет считаться равным одному периоду, который соответствует стандартному сроку действия договора имущественного страхования. Заметьте, что, хотя потеря бонуса растягивается на много лет, потребитель действует на основании данных о текущей ее стоимости, детерминированной на момент возникновения убытка, следовательно горизонт анализа, равный одному периоду не противоречит нашему подходу.

Классическое условие оптимальности. Для начала рассмотрим классический подход, при котором считается, что в договоре страхования не содержится условий о BMS. Тогда необходимым условием того, что потребитель приобретет страховую защиту с(.) , уплатив премию р является:

Eu(w – X + c(X) – p) ³ Eu(w – X)         (3)

Другими словами, потребитель предпочтет приобрести страховую защиту с(.), если ее ожидаемая полезность больше или равна ожидаемой полезности ее отсутствия. Заметьте, что здесь случайная величина Х представляет собой полную подверженность потребителя риску, включая не только неопределенность величины убытка, но и неопределенность его возникновения. Распределение X, f(x), поэтому является смесью, содержащей вероятность того, что риск не реализуется, в точке х=0 и непрерывное распределение при х > 0, соответствующее возникновению одного или нескольких убытков.

Разумеется может существовать более чем один вид страховой защиты, удовлетворяющий (3). Тогда оптимальным выбором страховой защиты будет тот, который будет максимизировать левую часть (3) в зависимости от изменения с(.) и р, причем здесь р, очевидно, зависит от с(.).

Оптимальное условие при наличии BMS. Теперь рассмотрим договор страхования с BMS. Теперь (3) перестает быть условием покупки страхования. Чтобы получить корректное необходимое условие приобретения страхования мы должны ввести в него функцию реального страхового возмещения, определенную в (2). Точнее необходимым условием, чтобы потребитель приобретет страховую защиту с(.) , уплатив премию р является:

Eu(w – X + c^*(X) – p) ³ Eu(w – X)         (4)

В (4) р определяется общими правилами BMS и является функцией с(.). Если (4) выполняется хотя бы для одного вида функции контрактного возмещения с(.), тогда оптимальным выбором страховой защиты будет та функция, которая максимизирует левую часть (4).

В условиях договоров страхования с BMS условие (4), разумеется, будет влиять на множество утверждений и выводов классической теории выбора страховой защиты. В Секциях 4 – 6 некоторые из этих классических утверждений будут представлены, а затем откорректированы с использованием эффекта реального страхового возмещения в условиях действия BMS.

4. Премия для состояния безразличия.

Классическое утверждение 1. Предположим ситуацию, когда имеется стандартный договор страхования без BMS. Максимальной премией, которую потребитель мог бы уплатить за конкретную функцию страхового возмещения, является та премия p=p_max, которая превращает "³" в "=" в (3). Премия p_max, следовательно, есть та премия, при которой страхователю безразлично покупать страхование или нет, ее поэтому можно назвать премией безразличия. Существование такой премии фактически – одна из аксиом теории полезности фон Неймана–Моргенштерна.

Функция полезности u(.) обычно предполагается выпуклой и монотонно возрастающей, т.е. u'(.) > 0 и и''(.) < 0, что означает, что потребитель считается избегающим риска. Отсюда, просто используя неравенство Иенсена, мы получаем, что

p_max> Ec(X)         (5)

Это есть одно из ключевых утверждений экономики страхования. Практической интерпретацией (5) является то, что потребитель согласен участвовать в несправедливой игре (честной игрой было бы p_max= Ec(X)).

Утверждение 1 при наличии BMS. Премия безразличия.
При наличии BMS премия безразличия удовлетворяет неравенству:

p_max> Ec^*(X)         (6)

Где с^*(.)задано в (1).

Доказательство: Из неравенства Иенсена следует, что u(w–EX) > Eu(w–X), поскольку u''(.)<0. Следовательно, знак равенства в (4) сохранится для некоторого p_max> Ec^*(X).

Практическая интерпретация (6) фактически такая же, как и для (5), т.е. избегающий риска потребитель согласен участвовать в нечестной игре, однако уровень нечестности премии в 5. Оптимальная страховая защита для фиксированной функции премии.

Два вводных вопроса в секции 1 касались проблемы рационального выбора при покупке страхования из фиксированного набора полисов с BMS, предложенного страховщиком. Другими словами условия договора страхования предполагаются заданными экзогенно, и страхователь не может на них влиять. Этот подход отражает ситуацию на массовых страховых рынках, где способность потребителя влиять на условия договора находится в определенных рамках. Следующее классическое утверждение и соответствующее ему утверждение для BMS относятся именно к такой ситуации. Оговоренное договором возмещение, как предполагается, имеет форму эксцедента убытка, которая, пожалуй, наиболее часто встречается на мировом страховом рынке.

Классическое утверждение 2.
Рассмотрим классический договор страхования, т.е. без BMS. Предположим, что оговоренная в договоре функция страхового возмещения имеет вид
c(X) = max(X–d, 0), где d ³ 0 – указанная в договоре франшиза; а уплачиваемая по этому договору премия p(d) равна (1+ g) Ec(X) + k, где g ³ 0 – рисковая надбавка, а k ³ 0 – фиксированная плата, покрывающая издержки страховщика. Если g = 0 ( и w > p(d) + d ), а k не слишком велика, тогда покупка наибольшей страховой защиты всегда является оптимальным выбором, т.е. d = 0 – оптимальный выбор. Если k очень велика, единственный вариант – отказ от страхования.

Это классическое утверждение было выведено в Borch (1990), с. 33-34. Как мы увидим ниже, это утверждение о максимальной защите остается в силе и для договора с BMS. Однако, при наличии BMS определение максимальной страховой защиты несколько иное.

Утверждение 2 для договора с BMS.
В условиях договора c BMS предположим, что договорная функция страхового возмещения имеет вид
c(X) = max(X–d, 0), где d ³ 0 – указанная в договоре франшиза; а премия по нему есть p(d) = (1+ g) Ec^*(X) + k, где g ³ 0 – рисковая надбавка, а k ³ 0 – фиксированная плата, покрывающая издержки страховщика. Если g = 0 ( и w > p(d)+ z(d)+ d ), а k не слишком велика, тогда оптимальным выбором всегда оказывается покупка максимальной реальной страховой защиты, т.е. оптимальным является выбор такого значения d, чтобы z'(d) = –1. Если k слишком велика, то единственный вариант – не заключать договор страхования.

Замечание. Вовсе не обязательно, что страховые компании в явном виде рассчитывают Ec^*(X) в формуле для премий p(d) = (1+ g) Ec^*(X) + k. Однако они делают это в неявном виде, поскольку они используют данные о реальных убытках, на которые воздействует эффект бонусного голода страхователей, в качестве входных данных для процедуры расчета премий.

Доказательство. Из (1) вытекает выражение для реального страхового возмещения:
c^*(X) = max(X–d – z(d), 0), очевидно, что здесь дополнительная франшиза, z(d), возникающая из-за бонусного голода, является функцией d, поскольку p(d) зависит от d.

Оптимальная страховая защита максимизирует левую часть (4). Следовательно:

(7)

Первым обязательным условием максимума является U'(d) = 0. Поэтому напрямую дифференцируя (7) находим:

       (8)

Из формулы для расчета премии имеем:

       (9)

Откуда следует:

     (10)

И поэтому:

 (11)

Теперь, подставив (10) и (11) в (8), и проведя некоторые преобразования, получаем:

(12)

Поскольку u'(.) > 0 и u''(.) < 0, мы видим из (12), что при g = 0 и w > p(d)+ z(d)+ d: U'(d)=0 тогда, и только тогда, когда z’(d) = –1.

 (6) иной чем в (5).

Из (12) мы также, в общем случае, получаем:

U'(d) > 0 , когда z'(d) < –1.
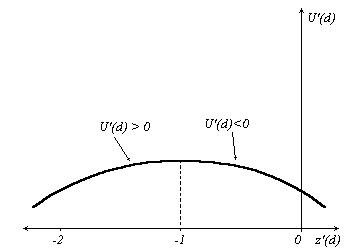
U'(d) < 0 , когда z'(d) > –1.

Что и подразумевает, что z'(d) = –1 есть точка максимума для U(d), как это показано на рисунке 1.

Рисунок 1.

Следовательно, при g = 0 и w > p(d)+ z(d)+ d значение d, при котором z'(d) = –1, является оптимальным решением задачи о выборе страховой защиты, т.е. максимизирует полезность потребителя.

Пусть D(d) = d+ z(d) есть реальная франшиза. Тогда D'(d) = 1+ z'(d), и поэтому D'(d) = 0 при z'(d) = –1. Поскольку D'(d) < 0 при z'(d) < –1 и D'(d) > 0 при z'(d) > –1, то z'(d) = –1 есть точка минимума D(d). Причем этот минимум больше нуля, поскольку z(d) > 0 для всех d ³ 0.

Из (10) мы одновременно получаем, что p'(d) = 0 тогда и только тогда, когда z'(d) = –1. Поскольку p'(d) > 0 при z'(d) < –1 и p'(d) < 0 при z'(d) > –1, то при z'(d) = –1 мы имеем точку максимума p(d).

Отсюда мы можем сделать окончательный вывод, что z'(d) = –1 означает максимум премии p(d) и минимум реальной франшизы d+ z(d), что вместе означает максимум реальной страховой защиты. Другими словами, максимум реальной страховой защиты эквивалентен максимуму ожидаемой полезности для потребителя, при условии, что в функции премии g=0.

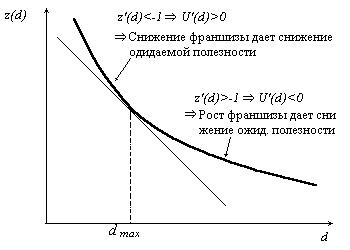
Заметьте, что может существовать более чем одно значение d, при котором z'(d) = –1; обозначим эти значения d_max. Все другие значения, отличные от d_max дают меньшую ожидаемую полезность с точки зрения страхователя. Рисунок 2 представляет собой графическую интерпретацию этого результата, показывая существование касательной с наклоном z'(d) = –1, касающейся графика z(d) в точке d_max, дающей максимум ожидаемой полезности. Для простоты на этом графике предположено существование только одной точки d_max, удовлетворяющей z'(d) = –1, а также то, что договор страхования с BMS предполагает уменьшение скорости уменьшения премии при росте франшизы d.

Рисунок 2.

Правила BMS, заложенные в договор, рыночная процентная ставка l и индивидуальный уровень премий, действующие в момент приобретения, определяют индивидуальные значения d_max, а также то, что при иных значениях d ожидаемая полезность будет меньше. Этот весьма сложный и зависящий от индивидуальных характеристик вывод отражает до некоторой степени реальную ситуацию, возникающую при покупке страхования: И страховщик и страхователь считают очень сложным предлагать и выбирать индивидуальную величину франшизы в договоре с BMS. А если уменьшение премии, вызванное ростом франшизы имеет верхний предел, как это бывает у большинства страховщиков, тогда для некоторых потребителей может вообще не существовать индивидуальное значение d_max. Следовательно, эти потребители должны, вероятно, вообще отказаться от страхования. Этими потребителями обычно являются потребители с низким уровнем бонуса, высоким уровнем премий, и жесткими правилами штрафа, когда рыночная процентная ставка l низка. С другой стороны, потребители с высоким уровнем бонуса, низкми премиями, мягкими правилами штрафа и при высокой l будут, очевидно, приобретать страхование, устанавливая в договоре франшизу на уровне d_max.

Заканчивая эту Секцию мы сделаем вывод относительно нашей модели с BMS: Если согласно договору страховое возмещение имеет форму эксцедента убытка, а в функцию премии не включена рисковая надбавка, тогда существует определенный наилучший выбор страховой защиты, который максимизирует функцию ожидаемой полезности по сравнению с другими вариантами. Оптимальным страховой защитой по договору будет та, которой соответствует максимальная реальная страховая защита, т.е. та, когда z'(d) = –1. Этот вывод полностью симметричен соответствующему выводу для классического случая, когда оптимальным будет максимальная (договорная) страховая защита.

Заметим, что хотя мы в нашей модели определили реальную франшизу как NPV потерянного бонуса за бесконечный промежуток времени, полученное правило действует и для других предположений относительно z(d). Единственным условием является некоторая зависимость z(d) от d.

6. Страховая защита оптимальная по Парето.

Заключение в Секции 5 ведет нас к более общему подходу к определению оптимальной страховой защиты в случае наличия BMS в договоре страхования. Здесь мы сформулируем наш основной вопрос иначе: “Что есть оптимальность договора страхования с BMS на страховом рынке?” Или даже более критично: “Возможна ли такая оптимальность вообще?” Для решения этих задач необходима методика анализа Оптимальности по Парето, когда и страхователь и страховщик анализируются с точки зрения распределения риска между ними.

Рассмотрим договор имущественного страхования с BMS. Необходимое условие для того, чтобы страховщик предложил реальное страховое возмещение
c^*(X) = max(c(X) – z(p), 0) за премию p, очевидно:

Eu₀(w₀ – c^*(X)+ p) ³ u₀ (w₀)         (13)

Где u₀ (.) – функция полезности для страховщика, удовлетворяющая условиям: u₀'(.) > 0 и u₀''(.) ³ 0; w₀ – исходное богатство страховщика, а р следует правилам общей BMS. Чтобы договор страхования, включающий BMS, был приемлем и для страховщика и для страхователя должны одновременно выполняться (13) и (4). Если таковой договор существует, тогда оптимальным по Парето будет тот, который максимизирует полезность обмена риском для страхователя и страховщика, т.е. договор страхования, который максимизирует левые части (4) и (13). Эта простая модель ниже будет называться стандартной моделью обмена риском, которая, по сути, просто часть классической 1960-теоремы Оптимальности по Парето Borch’а. В рассматриваемой модели эта теорема фактически говорит, что достаточным условием Оптимальности нашего договора по Парето является существование положительных констант k₀ и k таких, что:

k₀ u₀'(w₀ + p – c^*(X)) = k u'(w– p – X + c^*(X))

Что выражает математически общую линейную максимизацию левых частей (4) и (13). Желающие выяснить детали могут смотреть Borch (1990), Глава 2.5 или Aase (1993), Глава 3. Итак мы имеем…

Утверждение 3 для договоров с BMS. Договор страхования с BMS не может быть оптимальным по Парето в рамках традиционной модели обмена рисками.

Доказательство. Прямое применение Теоремы Borch’а дает нам условие оптимальности по Парето первого порядка для правила распределения риска между страховщиком и потребителем:

u₀'(w₀ + p – c^*(X)) = [k/k₀ ] u'(w– p – X + c^*(X))         (14)

Где k₀ и k – произвольные положительные константы. Согласно Aase (1993), Глава 8, дифференцирование (14) по Х даст нам:

(15)

Где R и R₀ – меры Arrow-Pratt’a для абсолютной несклонности к риску для потребителя и страховщика, соответственно. Если и страховщик и потребитель не склонны к риску, тогда напрямую из (15) мы получаем общий критерий оптимальности по Парето:

       (16)

С другой стороны, в ситуации, когда в договор страхования включена BMS, имеем c^*(X) = max( c(X) – z(p), 0 ). Следовательно производная c^*(X) по Х обращается в нуль при c(X) £ z(p), а значит общий критерий оптимальности (16) не выполняется.

Для стандартного договора страхования соответствующее утверждение приведено ниже, его доказательство, которое проводится образом, подобным только что использованному нами, можно найти в Aase (1993), Глава 8.

Классическое утверждение 3. Оптимальное по Парето распределение риска для договора страхования без BMS в стандартной модели обмена рисками включает ненулевое взаимное страхование. Однако, если в функцию договорного страхового возмещения включена франшиза, то такое страховое возмещение не может быть оптимальным по Парето.

Предложение 2 из Holtan (2001) утверждает, что независимо от наличия франшизы в договоре, функция реального страхового возмещения при наличии BMS всегда включает индивидуальную для каждого страхователя франшизу. Поэтому, в условиях стандартной модели обмена риском, интуитивно понятно, что утверждение о неоптимальности страхового договора с франшизой, остается в силе для любого договора страхования с BMS.

В Aase (1993), Глава 8 был сделан вывод, что стандартный договор страхования с франшизой может быть оптимальным по Парето только в моделях где присутствует хотя бы одно из списка: затраты при обмене рисками, моральный вред, асимметрия информации, альтернативные предпочтения (т.н. звездообразная полезность ). Стандартными ссылками здесь могут быть: Arrow (1974), где была введена постоянная доля затрат, чтобы продемонстрировать оптимальность франшиз; Raviv (1979), где было показано, что франшиза является оптимальной по Парето тогда и только тогда, когда затраты на страхование зависят от страховой защиты; Rothschild, Stiglitz (1976), где была введена асимметрия информации и обнаружено, что потребители с низким риском предпочтут высокие франшизы; Holmstrøm (1979), где было обнаружено, что моральный вред ведет к росту франшиз.

Эти дополнения для стандартной модели обмена риском в общем соответствуют предназначениям BMS на страховом рынке:

1. Антиселекция. BMS позволяет измерить и сгладить асимметрию информации за счет индивидуальной апостериорной тарифиации.
2. Моральный вред. BMS позволяет уменьшить вероятность претензий, поскольку штрафует за них.
3. Затраты. BMS уменьшает административные расходы, возникающие при рассмотрении убытков.

Поскольку ни один из этих элементов не был введен в модель обмена рисками в этой статье, мы можем сделать лишь такое предположение:

Предположение. Договор страхования с BMS может стать оптимальным по Парето, если модель обмена рисками учитывает хотя бы одно из предназначений BMS, (1-3).

Предложения 3 и 4 из Holtan (2001) утверждают, что функция страхового возмещения для договора страхования c BMS без франшизы эквивалентна функции страхового возмещения для стандартного договора страхования с индивидуальной франшизой. Следовательно, формально доказать наше предположение в случае отсутствия франшизы в договоре должно быть не сложно.

С другой стороны, если мы не ограничиваемся договорами без франшизы, тогда величина потерянного бонуса зависит от индивидуального выбора франшизы в договоре, см. Секцию 5. Эта зависимость усложняет анализ оптимальности по Парето и, следовательно, усложняет доказательство.

В качестве заключительной ремарки к сказанному выше мы можем отметить, что обычные франшизы используются на страховом рынке в качестве основного инструмента для уменьшения вероятности убытка (морального вреда) или затрат на урегулирование убытков. Поэтому основным предназначением договоров с BMS является решение проблемы антиселекции вызванной индивидуальной асимметрией информации. (Хотя в Holtan (1994) предлагалась модель с высокими франшизами, финансируемыми в течение некоторого промежутка времени, как альтернатива BMS. ) Отсюда следует основное правило: BMS должна использоваться только тогда, когда индивидуальная статистика убытков является важным параметром риска в рассматриваемом виде страхования.

7. Саммари.

В этой статье были получены некоторые новые факты относительно оптимальности страховой защиты при наличии BMS в договоре страхования, и они были сравнены с соответствующими классическими утверждениями для стандартных договоров страхования. Теоретической основой была модель ожидаемой полезности, однако ни антиселекция, ни моральный вред, ни транзакционные издержки не были включены в нее. При предположении о том, что страховое возмещение имеет форму эксцедента убытка, и том, что в премию не включена рисковая надбавка, было показано, что максимальная реальная страховая защита приносит максимальную полезность потребителю. Этот результат находится в соответствии с классическим результатом верным для договоров страхования без BMS. С другой стороны, в рамках той же теоретической модели, было показано, что договор с BMS не может быть оптимальным одновременно для страхователя и страховщика, т.е. не может быть оптимальным по Парето. Предположение из Секции 6, которое не было формально доказано, утверждает, что договор с BMS может стать оптимальным по Парето, только если в модель обмена рисками включены антиселекция, моральный вред и/или транзакционные издержки.