Оптимальное финансирование убытков для страхователя находящегося в BMS.

Анализируемая модель включает стратегию бонусного голода, в которой потребитель выбирает альтернативу финансирования, которая приносит наибольшую прибыль, т.е. альтернативу с наименьшей процентной ставкой. Соответственно потеря бонуса после заявления убытка представляется в виде процентной ставки, которую страхователь платит страховщику. В работе, в рамках этой модели, обнаружено существование функции реального страхового возмещения, а также функции относительной стоимости для каждого потребителя. Набор свойств договоров в условиях BMS был представлен и рассмотрен в работе. Конкретный пример BMS и функции страховой компенсации иллюстрируют теорию в условиях близких к страховой практике.

Соглашение между страхователем и страховщиком, регулирующее их взаимные обязательства в соответствии с условиями данного вида страхования, или соглашение, по которому одна сторона (страховщик) принимает на себя за обусловленное вознаграждение (страховая премия) обязательство возместить убытки другой стороны (страхователя), происшедшие вследствие предусмотренных в страховом договоре опасностей и случайностей (страхового случая), которым подвергается застрахованное имущество.

Система Бонусов и Штрафов (Бонус-Малус, BMS).

Система скидок к базисной тарифной ставке, с помощью которой страховщик уменьшает страховую премию, если в отношении объекта страхования не наблюдалась реализация страхового риска; система надбавок к базисной тарифной ставке, если в отношении объекта страхования обнаружилась реализация страхового риска. Обычно используется в Автомобильном Страховании. При обязательном страховании определяется законом.

Бонусный голод.

Термин для обозначения феномена сокрытия убытков страхователями с целью понижения будущих страховых премий. Является специфическим свойством договоров страхования

Реальное Страховое Возмещение.

Сумма, выплачиваемая страховщиком по имущественному страхованию и страхованию ответственности в целях компенсации ущерба вследствие страховых случаев. Величина страхового возмещения определяется в основном двумя способами: 1) при ответственности по первому риску убытки в пределах страховой суммы (первый риск) возмещаются полностью. Ущерб, превышающий эту сумму, не возмещается; 2) при пропорциональной ответственности, напротив, учитывается величина ущерба относительно стоимости имущества. Также учитывается наличие франшизы и др. факторы. Страховое возмещение не может превышать страховой суммы. Страховщик, осуществивший выплату С.в., приобретает право регрессного иска к причинителю вреда.

Реальная франшиза.

Сумма ущерба, которая вычитается из суммы страхового возмещения и покрывается страхователем

Относительная функция издержек.

Оптимальное финансирование убытков.

1. Введение.

Должен ли потребитель страховой услуги оплачивать убыток самостоятельно или должен заявить о нем страховщику? Этот вопрос является фундаментальным в случае договоров с условиями Бонус-Малус, т.е. в случае с договорами страхования в которых ценообразование производится на основании данных об убытках для рассматриваемого страхователя или данных об отсутствии таковых; примером таких договоров являются договоры автомобильного страхования (ОСАГО). Общая тенденция такова, что страхователи самостоятельно оплачивают небольшие убытки, чтобы избежать повышения премий в будущем, этим объясняется уместность заданного нами вопроса. Эта тенденция получила название бонусный голод страхователя. Бонусный голод неоднократно становился предметом дискуссии и анализа в актуарной литературе. Например смотри Lemaire (1995), глава 7, стр. 101-102, где содержится частичный обзор подобной литературы. Чем более жесткими являются правила штрафов, чем выше премии и чем меньше убытки, тем более остро стоит перед страхователем проблема бонусного голода; и наоборот. Предназначение этой статьи обнаружить и описать то, как эффект бонусного голода может быть учтен в модели оптимального финансирования убытка с точки зрения страхователя в условиях BMS.

Вопрос оптимального финансирования убытка актуален не только в момент возникновения убытка, но и в момент покупки страхования. Если выгодно сообщать страховщику об убытках лишь иногда, тогда зачем покупать такое страхование. Фактически, этот вопрос является частью общей проблемы приобретения оптимальной страховой защиты, который всесторонне изучался в страховом экономиксе. В частности в Holtan (2001) этот вопрос рассматривался для страхования при наличии BMS. Но чтобы сделать это мы должны в первую очередь предложить концепцию договора страхования при наличии BMS, что является одной из целей этой статьи.

Данная статья имеет следующую структуру: Секции 2 и 3 рассматривают договор общего страхования и стратегию бонусного голода страхователя. Секция 4 демонстрирует наличие функции реального страхового возмещения для всех договоров страхования при наличии Бонус-Малус поправок для премии. Секция 5 демонстрирует наличие функции относительной компенсации для потребителя и ее основные свойства. Секции 6 и 7 иллюстрируют некоторые идеи из Секций 4 и 5, если сделаны некоторые предположения о BMS и функции страхового возмещения. В Секции 8 сделаны некоторые заключительные ремарки.

2. Договор страхования в общем страховании.

Предположим, что потребитель страхования подвержен риску Х, где Х – случайная величина имеющая при x>0 функцию плотности f(x). Договор страхования характеризуется непрерывным процессом премий p(t), передаваемых страхователем страховщику в момент t, а также страховым возмещением с(х), передаваемым в обратную сторону, если произойдет убыток Х=х. Таким образом возмещение с(х) называется договорным возмещением. А допустимая функция договорного возмещения удовлетворяет 0 £ с(х) £ х при всех х³ 0. Это ограничение отражает тот факт, что если нет убытка, то нет возмещения ( с(0) = 0 ), а также то, что страхователь не должен получать прибыль от игры на своем риске ( с(х) £ х ).

3. Стратегия бонусного голода.

Пусть процесс премий p(t) зависит системы бонусов и штрафов. В принципе BMS увеличивает премию для страхователя, если убыток был возмещен страховщиком, и уменьшает ее, если оплаченных страховщиком убытков не было. Увеличение премии называется потерей бонуса и обычно зависит только от числа убытков, не учитывая их величину. Поэтому страхователь зачастую может сэкономить, оплачивая убыток самостоятельно, чтобы избежать увеличения премий в будущем, вместо того чтобы сообщить об убытке страховщику и потерять бонус. Данный феномен получил наименование бонусный голод (bonus hunger ). После возникновения убытка перед страхователем возникает проблема выбора наиболее выгодного способа финансирования убытка. Тривиальная теория инвестиций решает подобную проблему, используя в качестве критерия процентную ставку финансирования, т.е. потребитель должен предпочесть тот способ финансирования, которому соответствует минимальная процентная ставка.

Чтобы определить стратегию ( правило принятия финансовых решений ) страхователя в BMS, мы используем следующие обозначения и предположения: Премия, уплачиваемая в момент времени t, после того как в момент s произошел убыток, обозначается p₁(s + t), если об убытке было сообщено страховщику; или p₀(s + t), если об убытке не сообщалось. Предполагается, что p₀(s + t) и p₁(s + t) будут непрерывными не стохастическими процессами премий для всех t>0.

Определение 1. Если убыток имел место в фиксированный момент времени s и величина убытка Х=х также была фиксирована, тогда постоянная норма дисконтирования d(x), определенная выражением (где рассчитывается NPV): 

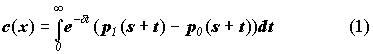
Является относительной мерой бонуса, потерянного при наступлении убытка.

Норма дисконтирования d(x) Î ( -¥, ¥ ) по определению является эффективной процентной ставкой для страхового возмещения. Чтобы выбрать оптимальный способ финансирования при возникновении убытка страхователь должен сравнить процентную ставку для страхового возмещения с процентной ставкой для других способов финансирования, среди которых можно выделить самостоятельное финансирование убытка за счет накоплений, за счет займа или за счет комбинации займа и накоплений, в зависимости от ликвидности страхователя. Пусть l₁ – процентная ставка по кредиту, l₂ – процентная ставка (доходность) по накоплениям в момент возникновения убытка; предположим, что l₁ и l₂ – положительные параметры, не меняющиеся во времени. Тогда детерминированная процентная ставка для самофинансирования убытка, l, при условии, что доля убытка b Î [0; 1] финансируется за счет кредита, определяется следующим образом (для простоты мы не учитываем налоги):
l = b l₁ +(1– b) l₂

Следовательно, стратегия бонусного голода для страхователя может быть одной из следующих:

• Если d > l Þ Самофинансирование;
• Если d < l Þ Убыток оплачивается страховщиком;
• Если d = l Þ Страхователю безразлично какую из двух альтернатив предпочесть.

4. Функция реального страхового возмещения.

Очевидно, что потеря бонуса при наступлении убытка оплачивается страхователем, а не страховщиком. В принципе, этот факт позволяет рассматривать потерю бонуса, как франшизу, которую страхователь постепенно выплачивает страховщику. Следовательно, реальная франшиза для страхователя есть сумма франшизы, указанной в договоре, х–с(х) и потери бонуса. Тогда мы можем определить критическую точку реальной франшизы, как величину убытка, при которой страхователю безразлично какой способ финансирования убытка использовать, т.е. такую, что d = l. Очевидно, что существование реальной франшизы означает существование реального страхового возмещения, которое отличается от прописанного в договоре возмещения с(х). Точное значение реального возмещения и франшизы определяется следующим образом:

Из формулы (1) мы, при d = l, можем определить фиксированное z: 

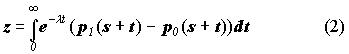
Здесь z является константой, так как величины l₁, l₂, p₀(s + t) и p₁(s + t) не являются случайными.

Из формул (1) и (2) мы можем вывести следующую модификацию стратегии бонусного голода:

• Если d > l Þ c(x) < z Þ Самофинансирование;
• Если d < l Þ c(x) > z Þ Убыток оплачивается страховщиком;
• Если d = l Þ c(x) = z Þ Страхователю безразлично какую из двух альтернатив предпочесть.

Следовательно, если мы считаем, что страхователи всегда будут следовать оптимальной стратегии, мы получаем:

Определение 2. Реальное страховое возмещение, с^*(х), при возникновении убытка Х=х есть: c(x) – z при c(x) > z и 0 в остальных случаях.

Определение 3. Реальная франшиза, d^*(x) = x – с^*(х), при возникновении убытка Х=х есть: x – c(x)+ z при c(x) > z и x в остальных случаях.

x – c(x)+ z есть критическая точка реальной франшизы, где x – c(x) – величина договорной франшизы, а z – величина франшизы, связанная с потерей бонуса. Мы можем дать такое определение:

Определение 4. Договор страхования при наличии BMS имеет не только функцию страхового возмещения, c(x), определенную договором, но и функцию реального страхового возмещения с^*(х).

Из (2) можно видеть, что, чем ниже l, тем выше z, которое, согласно определению 2, означает более низкую реальную компенсацию с^*(х). Следовательно мы обосновали такое предложение:

Предложение 1. Уменьшение силы процентной ставки на рынке денег вызывает снижение реального возмещения, и следовательно делает страхование менее привлекательным для потребителей; и наоборот.

В рассматриваемых условиях существуют верхний и нижний лимиты для d^*(x), причем оба они больше нуля. Нижний лимит соответствует l ® ¥, т.е. тому, что относительная стоимость самостоятельного финансированию убытка стремится к бесконечности, в то время как верхний лимит определяется при l ® 0, т.е. когда относительная стоимость самостоятельного финансирования стремится к нулю.
Пусть z_min = lim_{l ® ¥} z и z_max = lim_{l ® 0} z. Тогда, согласно определению 3, нижний и верхний лимиты для d^*(x) определяются следующим образом:

0 < min{x, x– c(x)+ z_min} £ d^*(x) £ min{ x, x– c(x)+ z_max }       (3)

А согласно определению 2, мы также можем определить верхний и нижний пределы для с^*(х).

max{0, c(x)– z_max} < c^*(x) < max{0, c(x)– z_min }         (4)

Из (3) и (4) вытекают два важных предложения.

Предложение 2: Независимо от прописанной в договоре страхования функции страхового возмещения, функция реального возмещения будет всегда иметь индивидуальную для каждого страхователя франшизу.

Предложение 3: Функция страхового возмещения для договора страхования с BMS без франшизы, оговоренной в самом договоре, эквивалентна функции страхового возмещения для обыкновенного договора страхования, когда франшиза определяется индивидуальным образом.

Предложение 3 основывается на том факте, что функция реального возмещения max{0, c(x)– z} упрощается до max{0, x– z}, когда в договоре страхования с BMS отсутствует франшиза. Поскольку z в этом контексте – нестохастическая дополнительная величина франшизы, связанная с потерей бонуса, функция страхового возмещения max{0, x– z} по определению имеет ту же структуру, как в обычном договоре страхования с франшизой z.

Заметим во-первых, что, даже если z выплачивается в течение длительного периода времени путем увеличения премии в договоре с BMS, z, тем не менее рассматривается как фиксированная франшиза в момент возникновения убытка. И, не будем забывать, страхователи действуют так, как будто z есть фиксированная франшиза, поскольку они должны принимать решение в момент возникновения убытка. Во-вторых, заметим, z зависит от х через процесс премий, p(t), а также через правила BMS. Следовательно, существуют различные функции страхового возмещения max{0, x– z} для различных страхователей. Их существование, однако, не влияет на справедливость Предложения 3, поскольку в нем мы допустили индивидуальность франшиз в стандартных договорах страхования. Но в общем можно сказать:

Предложение 4. Существуют различные функции реального страхового возмещения для различных страхователей.

5. Функция относительных издержек.

Определение 1 в Секции 3 позволяет выразить процентную ставку для страхового возмещения при условии, что величина убытка уже известна. Если мы не знаем величину убытка, или, точнее говоря, она является случайной величиной, тогда и процентная ставка становится случайной. Множество значений этой случайной процентной ставки в зависимости от величины убытка мы можем назвать функцией относительных издержек. Следовательно эта функция определяется так:

Определение 5. Множество значений случайной величины процентной ставки d(Х) Î ( –¥, ¥ ) в зависимости от величины убытка Х, определенное функцией настоящей стоимости убытка: 

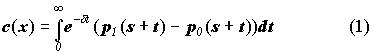
Называется функцией относительных издержек для любых возможных величин убытка.

Функция относительных издержек, ReCoF, выражает соотношение между любым возможным убытком х ³ 0 и соответствующей ему процентной ставкой страхового возмещения d. Практическая полезность этого соотношения очевидна: В начале страхового периода ReCoF предоставляет потребителю страховых услуг информацию о реальном страховом возмещении и реальной франшизе для него в случае, если в течение данного периода произойдет убыток. Рисунок 1 иллюстрирует обобщенную ReCoF, а также другую связанную с ней информацию. 

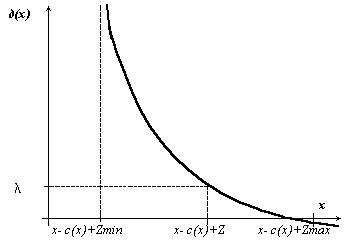
Рисунок 1. Обобщенная ReCoF – функция относительных издержек.

На Рисунке 1 мы видим, что функция относительных издержек (процентная ставка d) для страхового возмещения велика для малых убытков и мала для крупных, другими словами ReCoF является убывающей функцией. При этом дисконтирующий компонент в функции настоящей стоимости в определении 4 делает это свойство общим для всех существующих BMS.

На рисунке 1 на горизонтальной оси отмечены три важные значения величины убытка: Слева находится минимальное значение реальной франшизы x– c(x)+ z_min , а справа – ее максимальное значение x– c(x)+ z_max. Где-то посередине между ними находится x– c(x)+ z, которая при заданном d>(х) = l, является реальным значением франшизы для всех возможных величин убытка; при этом l – постоянная процентная ставка для самофинансирования убытка. Таким образом, мы видим, что информирование страховщика о мелких убытках, близких по значению к x– c(x)+ z_min может привести к росту до астрономических величин процентной ставки страхового возмещения для страхователя.

Наличие левого и правого значения на оси убытков приводит к возникновению трех вариантов, в случае возникновения убытка Х = х:

Исход 1: x < x– c(x)+ z_min Û 0 < c(x) < z_min

Исход 2: x– c(x)+ z_min < x < x– c(x)+ z_max Û z_min < c(x) < z_max

Исход 3: x > x– c(x)+ z_max Û c(x)> z_max

Общим для Исходов 1 и 3 является их независимость от параметра l. Другими словами, оптимальным выбором финансирования убытка в случае 1 всегда является самостоятельное финансирование, и этот выбор не зависит от l. Точно также, в случае 3 оптимальным выбором всегда является оплата убытка страховщиком; соответственно этот выбор также не зависит от l. Заметьте, что если убыток в случае 1 оказывается ниже оговоренной в договоре страхования франшизы, то страхователь не вправе требовать страхового возмещения, и следовательно, вообще не существует проблемы выбора способа финансирования.

Исход 2 является более сложным: Финансовый выбор здесь, в отличие от исходов 1 и 3, напрямую зависит от рыночного параметра l. В нашей модели, где принято, что l не зависит от времени, существуют два варианта для исхода 2:

Исход 2а: x– c(x)+ z_min < x < x– c(x)+ z Û z_min < c(x) < z

Исход 2б: x– c(x)+ z < x < x– c(x)+ z_max Û z < c(x) < z_max

Отсюда, согласно стратегиям бонусного голода из Секции 3, исход 2а означает оптимальность самостоятельной оплаты убытка; в то время как исход 2б означает оптимальность оплаты убытка страховщиком. Нужно заметить, что оптимальная финансовая стратегия при исходе 2 изменяется, если предположить, что l является случайной величиной; смотри Секцию 8, где находятся обсуждение и комментарии по этому поводу.

Из Определения 4 мы видим, что ReCoF также зависит от индивидуальных процессов премий p₁(s + t) и p₀(s + t). А эти процессы, в свою очередь, зависят от индивидуальных тарифных критериев для каждого страхователя. Следовательно мы допускаем существование различных ReCoF для различных страхователей, как и существование различных реальных франшиз и различных реальных возмещений. Мы также видим, что чем больше для страхователя изменения премий при потере бонуса, тем выше для него процентная ставка страхового возмещения, и, следовательно, тем выше реальная франшиза. При равной величине убытка Х = х, страхователь с большим изменением премии вынужден платить более высокую процентную ставку за получение страхового возмещения, чем страхователь с меньшим изменением премии. Следовательно, лица с высоким риском, наказываются не один раз (при назначении высокой премии), но дважды (за счет высокой премии и высокой процентной ставки страхового возмещения, которая эквивалентна высокой реальной франшизе).

Мы заканчиваем эту секцию следующим предложением, связанным с Предложением 4:

Предложение 5: Существуют различные функции относительных издержек для различных страхователей, но все эти функции – убывающие.

6. Теоретический пример.

Чтобы проиллюстрировать в дальнейшем задачу оптимального выбора финансирования убытков для страхователя, мы делаем следующие предположения относительно BMS, а также оговоренной договором функции страхового возмещения:

BMS: Пусть договор страхованию включает систему бонусов и штрафов, которая характеризуется непрерывной бонусной шкалой, где страхователь получает снижение премий в k^–1 раз, если за 1 времени не было убытков оплаченных страховщиком, и увеличение премии на фиксированную величину m после каждого убытка; 0 < k < 1; m > 0. Эта система является модификацией системы доверительности, описанной в Sundt (1988), и выбрана потому, что обладает простотой расчета. Еще одна версия этой системы в течение 10 лет (1987-97) использовалась в автомобильном страховании Норвежской страховой компанией Storebrand Ltd. (ныне норвежская часть if P&C Insurance), детали этой системы можно найти в Neuhaus (1988).

Давайте обозначим р премию, уплачиваемую страхователем в момент s, т.е. в момент возникновения убытка. Отсюда следует: p₁(s + t) = pk^t и p₀(s + t) = (p+m)k^t. Из (1) мы получаем:

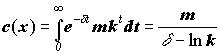
        (5)
Û при с(х) > 0 : d(x) = mc^–1(x)+ lnk         (6)

Заметим, что при с(х) = 0, d(x) не определено. А из (2) мы получаем:

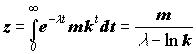
        (7)

Эффект бонусного голода в системе доверительности с геометрическими весами был изучен в Sundt (1988). Его бонусная стратегия была близка к нашей, но в отличие от нас он не обращал внимание на вопрос оптимального выбора финансирования для страхователя, т.е. он не использовал относительные издержки в качестве достаточного критерия для бонусного голода.

Страховое возмещение, согласно договору: Пусть функция договорного страхового возмещения является обыкновенной функцией эксцедента убытка, определяемой следующим образом:

c(x) = x – d при x > d ; в иных случаях c(x) = 0.

Где d – фиксированная величина безусловной франшизы. Теперь заданная нами BMS и функция договорного страхового возмещения позволяют нам вывести формулы следующие для d(x), c^*(x) и d^*(x):

d(x) = m(x– d)^–1+ lnk при x > d         (8)
с^*(x, k, m, l) = x– d – m(l – lnk)^–1 при x > d+ m(l – lnk)^–1         (9)

d^*(x, k, m, l) = d – m(l – lnk)^–1 при x > d+ m(l – lnk)^–1
d^*(x, k, m, l) = x в иных случаях         (10)

Здесь d+ m(l – lnk)^–1 оказывается реальной точкой эксцедента.

Нужно отметить, что формулы (8) – (10) содежат в себе предположение о фиксированной взаимосвязи между оговоренной в договоре франшизой d и процессами премий p₁(s + t) и p₀(s + t). Другими словами, в (8) – (10) d нельзя считать изменяемым параметром. В Секции 7 дискуссия по этой теме будет продолжена. А сейчас, используя (3) и (10), мы находим верхний и нижний пределы для d^*(х): 

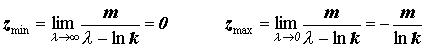
Отсюда следует:

0 < min( m, d ) £ d^*(x) £ min( x, d – m / lnk )         (11)

А из формул (4) и (9) вытекают верхний и нижний пределы для c^*(x):

max( 0, x– d+ m / lnk ) < c^*(x) < max( 0, x– d )         (12)

Как уже говорилось, представленная в этом примере BMS выбрана потому, что в ней легко провести аналитические расчеты показателей. Большинство используемых в настоящее время BMS весьма отличны от нее, и, соответственно, гораздо менее удобны при вычислениях. Поэтому единственным методом, применимым на практике, является численная оценка выражений (8) – (12) с помощью имитационного моделирования.

7. Числовые исследования.

Существует несколько способов численного анализа выражений (8) – (10), здесь мы вкратце рассмотрим два из них.

Способ 1.

Пусть k=0,87 ( как в старой BMS от Storebrand Ltd. ), и пусть d=0. Для этого случая в Таблице 1 показаны некоторые значения d(x, m) в диапазоне 500 £ x £ 5000 и 100 £ m £ 500.

Таблица 1.

Как ранее уже отмечалось, мы видим в таблице, что чем меньше величина убытка х, и чем больше увеличение премии m после убытка, тем выше процентная ставка d для страхового возмещения; и наоборот. Комбинация малого убытка и значительного прироста премий приводит к очень высокой процентной ставке страхового возмещения, что, разумеется, обозначает существенные финансовые потери для страхователя. Закрашенные ячейки выделяют те случаи, когда процентная ставка положительна. В данном случае минимальная величина реальной франшизы, x– c(x)+ z_min, равна нулю ( этот результат был аналитически получен в предыдущей секции ); а максимум реальной франшизы x– c(x)+ z_max равен –m/ lnk = m/0,139.

Способ 2.

Пусть как и выше k=0,87 и d=0. Пусть m принимает три различных значения: 100, 300 и 500. Для этого случая Рисунок 2 демонстрирует двумерную картину зависимости реальной франшизы d – m(l – lnk)^–1 от рыночной процентной ставки l (где 0 £ l £ 20%) для всех трех значений m. 

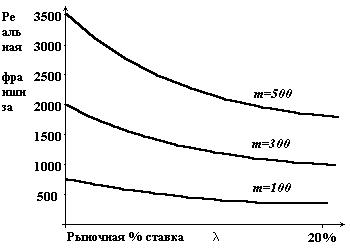
Рисунок 2.

На рисунке 2 мы видим, что уже утверждалось для общего случая, что чем выше рыночная процентная ставка, тем ниже реальная франшиза, и тем привлекательнее договор страхования для страхователей. Другими словами: возрастающая сила процентной ставки на рынке денег приводит к снижению реальной франшизы и увеличивает число убытков, заявляемых в страховую компанию; и наоборот. И как мы уже видели, этот эффект проявляется тем сильнее, чем больше увеличение премии после убытка.

Премии против франшизы в договоре.

Вернемся к неявному предположению о фиксированной зависимости между оговоренной в договоре страхования франшизой d и процессами премий p₁(s + t) и p₀(s + t) в выражениях (8) – (10) в Секции 6. В реальности, разумеется, величина франшизы влияет на премии. Следовательно, если мы желаем рассматривать d как изменяющийся параметр, мы обязаны сделать конкретные предположения о зависимости между премией и выбранной страхователем величиной d. Одним очень простым методом для этого было бы предположить, что премия p(d) равна wp = e^{–b d}. w можно считать здесь процентную скидку для франшизы d: p(0) = p и p(¥) = 0. Параметр b нужно подобрать таким образом, чтобы значения w выглядели разумно.

Сделанные изменения в законе определения премии дают p₀(s+t) = e^{–b d}pk^t и p₁(s+t) = e^{–b d}(p+ m)k^t. Соответственно, формула (5) из Секции 6 будет скорректирована:
c(x) = m e^{–b d} /(d – lnk), что приведет к похожим изменениям в формулах (6) – (12).

8. Заключительные ремарки.

Определение оптимального финансирования убытка в договоре страхования с BMS базируется на известном наборе предположений относительно поведения потребителя при покупке страхования. Два предположения могут вызвать споры: 1) Потеря бонуса z всегда оплачивается потребителем; 2) Потребитель всегда выбирает тот способ финансирования убытка, который приносит ему наибольшую прибыль.

Возражением против первого предположения может быть то, что стоимость потери бонуса может обратиться в нуль, если страхователь разорвет договор на следующий год после заявления убытка. Эта ситуация, однако учитывается в Определении 2 из Секции 4. Согласно Определению 2 в этом случае z = 0, поскольку p₁(s + t) и p₀(s + t) обращаются в нуль при разрыве договора. Соответственно, значение z базируется на индивидуальном поведении потребителя, как уже отмечалось в Секции 4. Если горизонт планирования страхователя равен году, как это происходит при разрыве договора, тогда договор страхования с BMS превращается в стандартный договор, без всяких штрафных санкций.

Возражение против второго предположения заключается в том, что страхователи могут выбрать финансирование убытка за счет страхового возмещения, даже если оптимальным выбором будет самофинансированию убытка. Следовательно с^*(х) из Определения 2 в Секции 4 становится отрицательным. Это скорее всего будет происходить, если потребитель вынужден прибегать страховому возмещению из-за своей низкой платежеспособности. Такую ситуацию можно исключить, если страховщик будет предлагать заем страхователю в дополнение к договору страхования и следовательно побеспокоится о его финансовых нуждах. Вероятно эти потребности страхователей недооцениваются ни страховщиками, ни банками. В Holtan (1995) приводятся некоторые идеи относительно организации финансовых услуг призванных удовлетворить эти потребности. Тем не менее, поскольку целью данной статьи является определение оптимального финансирования убытков при договоре страхования с BMS, второе предположение выглядит достаточно разумным.

Вопрос об оптимальном финансированию убытка напрямую связан с вопросом о приобретении страхования: Если лишь иногда выгодно обращаться в страховую компанию за возмещением в случае убытка, тогда зачем покупать страхование? Другими словами: Должен или не должен страхователь приобретать договор страхования с BMS? И если должен, то какой ковер он предпочтет? Этот вопрос приводит нас в традиционную сферу экономики страхования, к проблеме оптимального страхового покрытия. Статья Holtan (2001), которая базируется на данной статье и является ее прямым продолжением, анализирует этот вопрос для договоров с BMS.

И в качестве заключительной ремарки мы можем наконец поставить последний вопрос: Что это может означать для будущего и для дизайна договоров страхования с BMS. Хорошим выгладит прогноз, что различные BMS будут продолжать существовать на рынках, где индивидуальная статистика убытков является существенным параметром риска. Однако, эти системы будут становиться все более и более дружественными к страхователю, по мере того, как они будут становиться частью продукта, разработанного на основании маркетинговых исследований, см. например Holtan (1994) или Lemaire, Zi (1994), где такая система была предложена, обсуждена и проанализирована. С другой стороны, это приводит к возникновению более закрытых для потребителей систем поправок к премиям. Этим системам потребуются статистические данные, но уже не на уровне отдельного продукта, а на уровне отдельного потребителя. Другими словами, существует тенденция к одновременному использованию двух BMS воздействующих на каждого страхователя, одна из которых понятна страхователю, а другая оказывается для него “черным ящиком”. Эта тенденция является следствием повышения конкуренции на рынке имущественного страхования.